Geometry of the Complex Numbers: Rotations

Posted on Fri 23 March 2018 in Thesis

In the previous post in this series, we introduced a geometrical interpretation of the complex numbers as vectors in the 2-dimensional plane. That post also explained the geometrical significance of the addition of complex numbers as vector addition. In this post, we'll see how to interpret the multiplication of complex numbers geometrically.

Polar Coordinates in the Plane

Although we didn't make this explicit in the last post, our discussion of complex numbers as points or vectors in the two-dimensional plane has so far used two different coordinate systems. We first used the standard Cartesian coordinate system, plotting the real part of the complex number on the horizontal axis and the imaginary part on the vertical axis. This description works equally well if we consider the complex number as just a point or as a vector by drawing an arrow from the origin to that point.

The last post also discussed vectors in a physical context, as a way to interpret change in location (displacement), and in that context we instead described the vector using the magnitude and direction of the vector (e.g., traveling 5 miles southeast). Of course, this method gives us a way to name points as well - given a vector, the point that the vector describes is just the endpoint of the vector.

This method for naming points in the plane is known as the polar coordinate system. Instead of describing points using distances along perpendicular axes, this system describes points using the distance from a central point and the angle formed with some reference direction.

In order to explain polar coordinates we'll briefly put aside the complex numbers and just consider points in the plane as determined by \((x,y)\) coordinates. Given a point \((x,y)\) in Cartesian coordinates, what are its coordinates in the polar coordinate system? The relationship is pictured below:

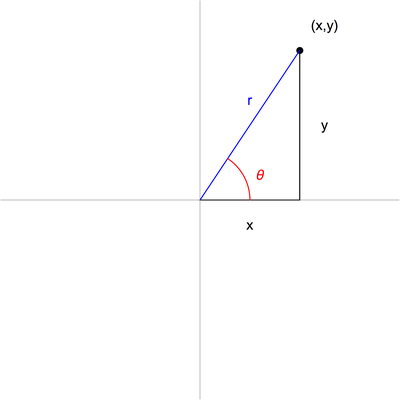
Polar Coordinate System

Polar Coordinate System

Here \(r\) (taken from radius) is the distance from the origin (the magnitude), and the Greek letter theta (\(\theta\)) gives the direction, as a counterclockwise angle from the positive x-axis.

This way to describe angles is different from the way we described directions in the last post. There, we used compass headings: due north was \(0^\circ\), which would correspond to the direction of the positive \(y\)-axis. In the polar coordinate system, the positive \(y\)-axis is at \(90^\circ\). Similarly, the positive \(x\)-axis is the \(0^\circ\) direction in the polar coordinate system, but it is measured as \(90^\circ\), or due east, with compass headings. The reference direction used to measure the angles doesn't ultimately make any real difference, so we'll use the traditional mathematical conventions of measuring angles starting from the positive \(x\)-axis.

Speaking of conventions, it's also worth pointing out that mathematicians generally use radians instead of degrees to measure angles. If once around the circle measures an angle of 360 degrees, the same angle is \(2\pi\) radians. For example, a right angle is either \(90^\circ\) or \(\pi/2\) radians. The distinction between measuring angles in degrees or radians can actually make an important difference in some situations (it's important in calculus, for example), but we won't encounter any such situations in this post, and so we'll mostly stick to degrees since they are more intuitive to most people.

In equations, the relationship is as follows. Given a point \((x,y)\) in Cartesian coordinates, its description in polar coordinates is

\begin{equation*} r = \sqrt{x^2 + y^2} \hspace{.25in} \theta = \arctan(y/x) \end{equation*}

where \(\arctan(x)\) is the inverse tangent function. Conversely, given a point \((r,\theta)\) in polar coordinates, its description in Cartesian coordinates is

\begin{equation*} x = r \cos \theta \hspace{.25in} y = r \sin \theta \end{equation*}

If \(r = 1\), then this relationship above is exactly the unit circle definition of the sine and cosine functions.

The Polar Form of Complex Numbers

We can now go back to considering complex numbers. So far, we've described complex numbers in terms of Cartesian coordinates. For the complex number \(z = a + bi\), the real part \(a\) gives to coordinate along the horizontal axis and the imaginary part \(b\) gives the coordinate along the vertical axis. Using the equations above, we can instead describe the complex number as a pair of numbers \(r\) and \(\theta\) in a polar coordinate system.

From the formulas, we have that \(r = \sqrt{a^2 + b^2}\). We've already encountered this expression before - this number is the same as \(\sqrt{z \bar{z}}\), where \(\bar{z} = a - bi\) is the complex conjugate of \(z\). We also used the symbol \(|z|\) to denote this value. In this context, the number \(|z|\) is called the modulus of the complex number \(z\). The value \(\theta = \arctan(y/x)\) also has a special name in the context of complex numbers, and is called the argument of \(z\), sometimes denoted by \(\text{arg}(z)\).

We therefore now have two different ways to describe a complex number. The first method uses its real and imaginary part, which corresponds to the \(z = a+bi\) description and Cartesian coordinates. The second method uses the modulus and argument, which correspond to magnitude and direction in polar coordinates. Using the formula to convert polar coordinates to Cartesian coordinates, we can write

\begin{equation*} z = |z|(\cos \theta + i \sin \theta) \end{equation*}

to express complex numbers in their so-called polar form.

Depending on the situation, one of these forms is usually a more convenient way to express complex numbers. For example, we've already seen that adding complex numbers in the Cartesian coordinate expression is fairly straightforward. If \(z_1 = a_1 + b_1 i\) and \(z_2 = a_2 + b_2 i\), then

\begin{equation*} z_1 + z_2 = (a_1 + a_2) + (b_1 + b_2)i \end{equation*}

It's not so easy to add complex numbers in polar form, however. If one were instead told only the modulus and argument of the complex numbers \(z_1, z_2\), then it's not immediately clear how to find the modulus and argument of the complex number \(z_1 + z_2\). The easiest way to find these values is usually to convert both \(z_1\) and \(z_2\) to their Cartesian coordinate expression, add them as above, and then convert back to polar form. (This is probably familiar to anyone whose main exposure to vectors is high-school physics. In that context, vectors are often given using magnitude and direction, and one of the easiest ways to add vectors in such a context is to find the \(x\) and \(y\) components of the vectors and add those separately. Finding the \(x\) and \(y\) components of a vector is exactly the same process as converting it from polar form to Cartesian form.)

On the other hand, we saw in a previous post that the multiplication of complex numbers, written in Cartesian coordinates, isn't exactly intuitive. The formula is that

\begin{equation*} (a_1 + b_1 i)(a_2 + b_2 i) = (a_1 a_2 - b_1 b_2) + (a_1 b_2 + a_2 b_1) i, \end{equation*}

which arises from treating \(i\) as a variable and gathering like terms, using the simplification that \(i^2 = -1\). This formula, though, will become much clearer when we consider the expression for the multiplication of complex numbers in polar form.

Multiplication of Complex Numbers in Polar Form

So how do we multiply complex numbers in polar form? If \(z_1, z_2\) are complex numbers, with moduli \(|z_1|, |z_2|\) and arguments \(\theta_1, \theta_2\), respectively, then their product is

\begin{align*} z_1 z_2 &= |z_1|(\cos \theta_1 + i \sin \theta_1)|z_2|(\cos \theta_2 + i \sin \theta_2) \\ &= |z_1||z_2|\Big( \big((\cos \theta_1)(\cos \theta_2)- (\sin \theta_1)(\sin \theta_2)\big) + i\big((\cos \theta_1)(\sin \theta_2) + (\sin \theta_1)(\cos \theta_2)\big) \Big) \end{align*}

This expression looks complicated, but can be simplified with a little knowledge of trigonometry. There are formulas that allow one to express the sine and cosine of the sum of two angles in terms of the sine and cosine of the angles being addded. Specifically, the following formulas are true for any pair of angles \(\theta_1, \theta_2\):

\begin{align*} \sin(\theta_1 + \theta_2) &= (\cos \theta_1)(\sin \theta_2) + (\sin \theta_1)(\cos \theta_2) \\ \cos(\theta_1 + \theta_2) &= (\cos \theta_1)(\cos \theta_2)- (\sin \theta_1)(\sin \theta_2) \end{align*}

Of course, these are exactly the expressions appearing above, and so we can finally express our multiplication formula in polar form as

\begin{equation*} z_1 z_2 = |z_1| |z_2| \big(\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)\big) \end{equation*}

This is the polar form for a complex number with modulus \(|z_1| |z_2| = |z_1 z_2|\) and argument \(\theta_1 + \theta_2\).

If you don't remember the various trigonometry identities, then understanding the derivation of the formula we gave above isn't really that important. What is important is that this formula finally gives a way to interpret the multiplication of complex numbers geometrically. We see that to multiply two complex numbers \(z_1\) and \(z_2\) in polar form, we multiply their respective moduli and add their arguments. This means that multiplication of complex numbers corresponds geometrically to stretching and rotating vectors in the the plane.

Let's illustrate this with a simple example. Let \(z = \sqrt{3} - i\), and let \(w = -2 + 2 \sqrt{3}i\). These are expressed in Cartesian form now, but using the formulas above one can show that in polar form

\begin{align*} z &= 2 \left(\cos(-30^\circ) + i \sin(-30^\circ) \right)\\ w &= 4 \left( \cos(120^\circ) + i \sin(120^\circ) \right) \end{align*}

that is, \(z\) has modulus \(|z| = 2\) and argument \(-30^\circ\), and \(w\) has modulus \(|w| = 4\) and argument \(120^\circ\). The product \(zw\) therefore has modulus \(|zw| = 2 \cdot 4 = 8\) and argument \(120 - 30 = 90^\circ\), and so can be expressed in polar form as

\begin{equation*} zw = 8 \left( \cos(90^\circ) + i \sin(90^\circ) \right) \end{equation*}

Expressed in Cartesian coordinates, this is

\begin{equation*} zw = 8i \end{equation*}

which could also be obtained by multiplying the expressions for \(z\) and \(w\) in Cartesian coordinates.

The geometrical interpretation is clearer when we plot \(z\), \(w\), and their product \(zw\) as vectors in the plane:

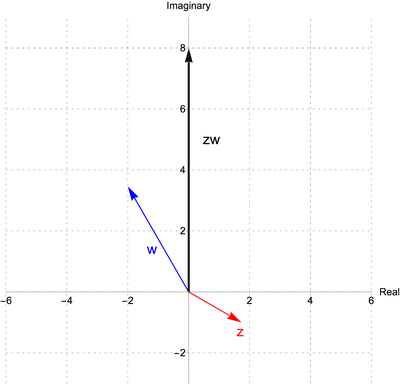
Geometrical interpretation of complex multiplication

Vector representation of \(z\), \(w\) and \(zw\)

Note in the image above that the length of \(zw\) is 4 times the length of \(z\), and twice the length of \(w\). The angles are a little harder to judge in this picture, but they match up as well - the angle between the \(zw\) and the positive \(x\)-axis is the sum the the angles that the vectors \(z\) and \(w\) make with that axis (the former angle being negative).

It's also helpful to think of multiplication as a transformation that one vector is performing on the other. For example, we could consider the product \(zw\) as taking the vector \(z\) and transforming it by the action represented by the complex number \(w\). That is, as \(w\) has a modulus of \(4\) and an argument of \(120^\circ\), it represents a transformation that consists of stretching any other vector to 4 times its length, then rotating it counterclockwise by \(120^\circ\). This is illustrated in the left picture below. This picture is the same as the picture above, but we mark the angles explicitly. Notice that the dashed red angle, which is the angle that we rotate \(z\) by to obtain the direction of \(zw\), is the same as the blue angle, the argument of \(w\).

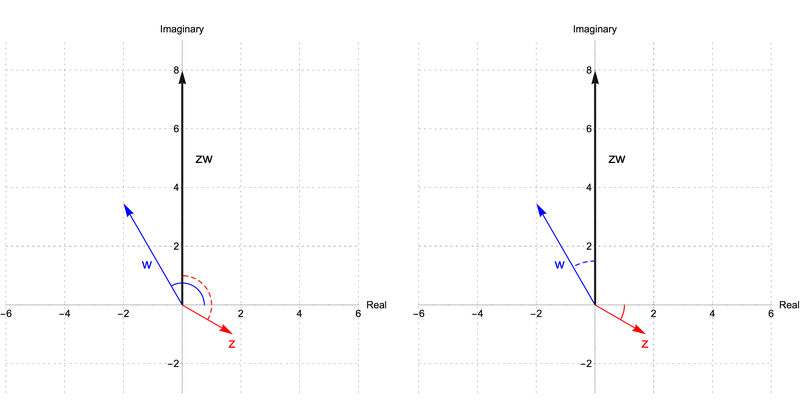Complex Multiplication as Rotation and Stretching Complex multiplication as a transformation of the plane

Of course, we could just as well consider the product \(zw\) as changing the vector \(w\) by the transformation represented by \(z\). As the modulus of \(z\) is 2 and its argument is \(-30^\circ\), this transformation consists of stretching by 2 and then rotating clockwise by \(30^\circ\). This is illustrated in the right picture above, where we see that the blue dashed angle that we must rotate \(w\) by to obtain the direction of \(zw\) has the same measure as the red angle, the argument of \(z\).

It's worth it to use this interpretation of complex numbers as transformations of the plane to think about the complex number \(i\) again. Under this interpretation, the complex number \(i\) corresponds to rotating the plane counterclockwise by \(90^\circ\). This means that the number \(i^2\) corresponds to rotation by \(90^\circ\), followed by rotation by \(90^\circ\), that is, rotation by \(180^\circ\). Of course, if you take the real axis and rotate it \(180^\circ\), the effect will be that every number will move to its opposite , e.g., 2 will move to \(-2\) and \(-4\) will move to 4. This transformation is the same as multiplying every real number by \(-1\). Therefore the algebraic expression \(i^2 = -1\), which before maybe seemed a little strange (how can the square of something be negative?) makes sense when considered geometrically.

Euler's Formula

This post is already a little long, and we've already explained the most important point for our future work, but it would be mathematical malpractice for me to discuss the multiplication of complex numbers without discussing "Euler's identity," which is considered by many to be one of the most beautiful equations in all of mathematics. Euler's identity is

\begin{equation*} e^{i \pi} + 1 = 0. \end{equation*}

This equation is famous for giving a simple relationship between 5 of the most important numbers in mathematics: Euler's number \(e\), the circle constant \(\pi\), the imaginary unit \(i\), the additive identity \(0\), and the multiplicative identity \(1\). (The equation could be more succinctly written as \(e^{i \pi } = -1\), but we cheat a little bit to be able to consider \(0\) and \(1\).)

This identity is actually a special case of a more general formula called Euler's formula. Given a real number \(\theta\), which we interpret as an angle measured in radians, we have that

\begin{equation*} e^{i \theta} = \cos \theta + i \sin \theta \end{equation*}

If we use this formula with the specific value of \(\theta = \pi\), we obtain the special identity above.

Right now, we basically have to take this formula as a definition of what \(e^{i\theta}\) means, so that \(e^{i\theta}\) is a different way to write the complex number with modulus 1 and argument \(\theta\). Using the interpretation we developed in the previous section, this means that \(e^{i\theta}\) is another way to represent the transformation of counterclockwise rotation by an angle of \(\theta\). This formula also gives us another way to write complex numbers in polar form - a complex number with modulus \(r\) and argument \(\theta\) is can be written succinctly as \(z = re^{i\theta}\). In this notation, the process of multiplication of complex numbers matches with the rules of multiplying expressions with exponents

\begin{equation*} (r_1 e^{i\theta_1})(r_2 e^{i\theta_2}) = r_1 r_2 e^{i(\theta_1 + \theta_2)} \end{equation*}

Described in this way, this formula perhaps doesn't seem very special - it's basically just a notational convenience. Truly understanding why this formula is correct and interesting requires calculus, and we won't get into that in this post. But as a first step down that path, the reader who remembers what a Maclaurin series expansion is encouraged to consider the Maclaurin series for \(e^{x}\) with \(x\) replaced with \(i \theta\) and compare the resulting expression to the Maclaurin series for \(\cos\theta, \sin\theta\).

Summary, and on to the Quaternions

This post marks the end of our consideration of complex numbers, at least for now. It's therefore helpful to summarize what we've discussed so far:

Complex numbers are numbers of the form \(a +bi\), where \(i^2 = -1\). Algebraically, they are interesting because they allow us to solve polynomial equations that don't have any real number solutions, like \(x^2 + 1 = 0\).
Geometrically, complex numbers can be visualized as points or vectors in the two-dimensional plane, with their real part \(a\) plotted along the horizontal axis and their imaginary part \(b\) plotted along the vertical axis. They can also be described using polar coordinates, in which case the distance from the origin is called the modulus and the angle with the positive real axis is called the argument.
Complex addition, when interpreted geometrically, is vector addition. Translate one vector to the tip of the other, and the sum vector is obtained by drawing an arrow from the base of the second to the tip of the first.
Complex multiplication, interpreted geometrically, is a transformation that consists of taking the vector associated to one of the complex numbers and then stretching and rotating it using the modulus and argument of the other complex number.

So what's next? Complex numbers give a compact way to describe geometric transformations in two dimensions, which leads to the question: what about three dimensions? Is there a way to define a multiplication operation of three-dimensional objects or vectors that has a natural geometrical interpretation? Can rotations in three dimensions be described neatly in such a way? The answer is yes, and this is done using the quaternions we've already discussed. In the next series of posts, we'll begin to understand more about vector geometry in three dimensions and how quaternions can be used to describe this geometry.